Hello

This page started life as a reference I was compiling for my own use and began with page 101 of the Reason Operation Manual pdf. I was curious about the exact characteristics of each waveform while I was using UI Software's Metasynth program and began to open up and analyze samples made by the Subtractor synth just for fun. After screen capturing each waveform, I also used Mac the Scope for the spectral analysis of the harmonic content and added that as well. I am in no way affiliated with Propellerhead and if any content here requires additional clarification on that point or violates anything I have not thought of, I can be reached here. My purpose is to give Reason users a resource so that maybe a few people might be inspired to explore more of the possibilities of this great software and share the results with the rest of us.

Subtractor: Virtual Analog?

The high prices commanded by some vintage analog music gear is testament to the popularity of the imperfect sound this equipment creates. In this day and age where 24-bit digital recording setups are fast becoming the norm in even small home studios, you can pay thousands for a 25 year old synth that originally sold for mere hundreds! Everyone seems to want that analog 'feel'. With the speed of todays computers, virtual synths running on PCs can now be used to emulate the sounds of some of this equipment and the Subtractor synth is perhaps one of the better examples of how a digital computer can act like dusty resistors and capacitors instead of a sterile digital signal generator.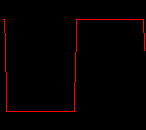

   
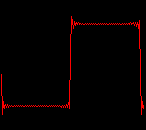
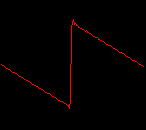
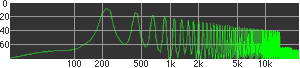
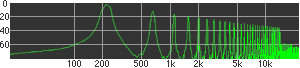
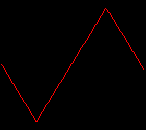
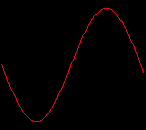
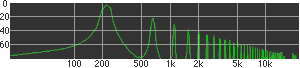
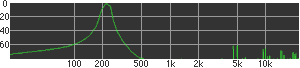
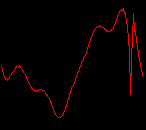
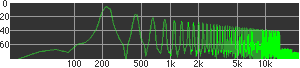
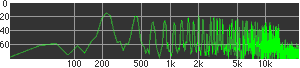
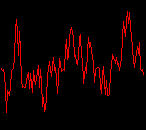
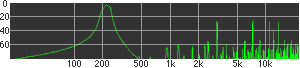
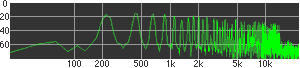
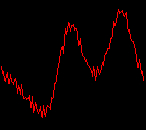
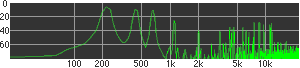
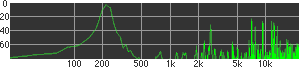
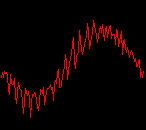
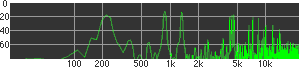
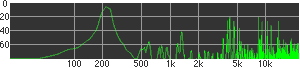
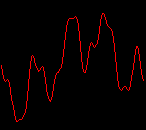
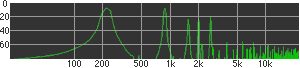
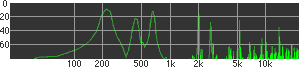
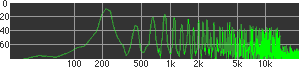
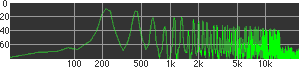
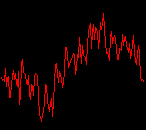
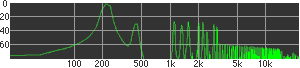
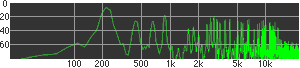
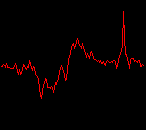
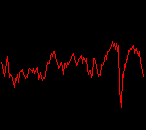
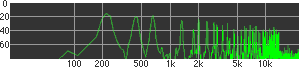
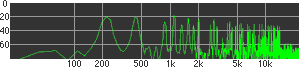
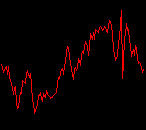
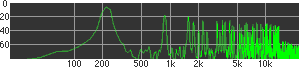
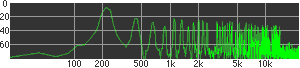
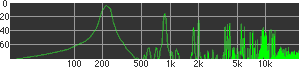
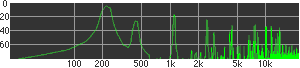
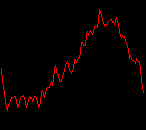
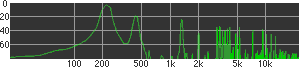
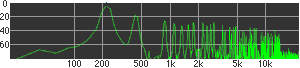
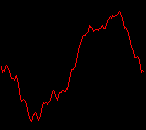
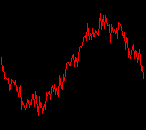
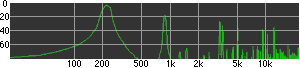
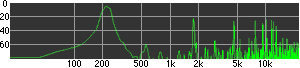
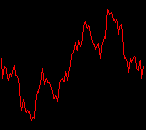
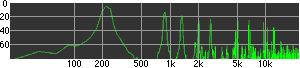
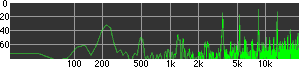
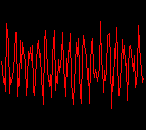
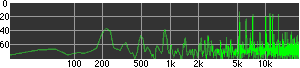
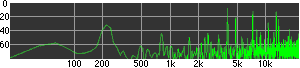
click waveforms to hear output

The waveform on the left was generated with MetaSynth from a pure mathematical formula. The Square wave is basically a funtion that has only two values, maybe a "-1" and "1" that change back and forth over time. In the digital world, it is then a simple affair for an oscillator to generate this 'function' and our picture on the left demonstrates this with the clean lines of the waveform free of transients. The waveform on the right however, has tiny imperfections at the corners of the wave's shape. Is something wrong? Well in the physical world, nothing is truly perfect and when an analog oscillator tries to produce a wave that abruptly changes values (-1 to 1 for example) it simply cannot happen without some distortion. This is because real semiconductors like capacitors and resistors cannot discharge or charge themselves with electricity at an instant; there is a microscopic amount of time needed to accomplish their tasks and the result of this can be observed here as the Gibbs Phenomenon. The result is a slightly different harmonic content (not shown, yet) where some of the higher frequencies are slightly enhanced.

What we are looking at below

Each waveform was recorded from the note A3 , or A below middle C, or 220 Hz. In each spectrogram you will notice the fundamental frequency peaks just to the right of the 200 Hz line. All the other peaks represent harmonics generated by the waveform, usually decending in amplitude as the distance from the fundamental increases. Click on each waveform to hear what it sounds like. Comments welcome.
Sawtooth
This waveform contains all harmonics and produces a bright and rich sound. The Sawtooth is perhaps the most 'general purpose' of all the available waveforms.		 Square
A square wave only contains odd number harmonics, which produces a distinct, hollow sound
Triangle
The Triangle waveform generates only a few harmonics, spaced at odd harmonic numbers. This produces a flute-like sound, with a slightly hollow character.		 Sine
The sine wave is the simplest possible waveform, with no harmonics (overtones). The sine wave produces a neutral, soft timbre.
Waveform 5
This waveform emphasizes the higher harmonics, a bit like a sawtooth wave, only slightly less bright sounding.		 Waveform 6
his waveform features a rich, complex harmonic structure, suitable for emulating the sound of an acoustic piano.
Waveform 7
This waveform generates a glassy, smooth timbre. Good for electric piano-type sounds.		 Waveform 8
This waveform is suitable for keyboard-type sounds such as harpsichord or clavinet.
Waveform 9
This waveform is suitable for electric bass-type sounds.		 Waveform 10
This is a good waveform for deep, sub-bass sounds
Waveform 11
This produces a waveform with strong formants, suitable for voice-like sounds.		 Waveform 12
This waveform produces a metallic timbre, suitable for a variety of sounds.
Waveform 13
This produces a waveform suitable for organ-type sounds.		 Waveform 14
This waveform is also good for organ-type sounds. Has a brighter sound compared to waveform 13.
Waveform 15
This waveform is suitable for bowed string sounds, like violin or cello.		 Waveform 16
Similar to 15, but with a slightly different character.
Waveform 17
Another waveform suitable for string-type sounds.		 Waveform 18
This waveform is rich in harmonics and suitable for steel string guitar-type sounds.
Waveform 19
This waveform is suitable for brass-type sounds.		 Waveform 20
This waveform is suitable for muted brass-type sounds.
Waveform 21
This waveform is suitable for saxophone-like sounds.		 Waveform 22
A waveform suitable for brass and trumpet-type sounds.
Waveform 23
This waveform is good for emulating mallet instruments such as marimba.		 Waveform 24
Similar to 23, but with a slightly different character.
Waveform 25
This waveform is suitable for guitar-type sounds.		 Waveform 26
This is a good waveform for plucked string sounds, like harp.
Waveform 27
Another waveform suitable for mallet-type sounds (see 23-24), but has a brighter quality, good for vibraphone-type sounds.		 Waveform 28
Similar to 27, but with a slightly different character.
Waveform 29
This waveform has complex, enharmonic overtones, suitable for metallic bell-type sounds.		 Waveform 30
Similar to 29, but with a slightly different character. By using FM (see page 104) and setting the Osc Mix to Osc 1, this and the following two waveforms can produce noise.
Waveform 31
Similar to 30, but with a slightly different character.		 Waveform 32
Similar to 30, but with a slightly different character.